triángulos, círculos y otras figuras geométricas, sin las cuales es humanamente imposible
comprender una sola palabra; sin ellos solo se conseguirá vagar por un oscuro
laberinto"
Galileo Galilei
En matemàticas, una espiral es una curva que se inicia en un punto central, y se va alejando progresivamente del centro al mismo tiempo va girando alrededor de él. La "espiral logarítmica" es conocida tambien por el nombre de "espiral de crecimiento", la podemos observar a menudo en la naturaleza.
El primero en hablar de ella fue René Descartes en el año 1638, quien un año después de la publicación de "La Géométrie", se va encontrar con la curva mecánica que responde al problema planteado por Galileo sobre la trayectoria de la caída de un cuerpo atraído por la tierra en rotación.
Descartes en 1638 comunicó sus investigaciones sobre esta curva a Mersenne.

Aunque Descartes y Torricelli habían iniciado su estudio, les faltaba la potente herramienta del cálculo para poder llevar a fin su descubrimiento.
Esto se consiguió en el siglo XVIII, gracias a Jacob Bernouilli, quien le dió el nombre de "espiral logarítmica" se quedó maravillado por la belleza de la figura la bautizó con el nombre de "Spira Mirabilis" (espiral maravillosa), asi tituló su obra dedicada a esta espiral.
Tanto le encantó que dejó escrito en su testamento que, en su lápida debería figurar una espiral logarítmica, y una inscripción en latin que dice:
"Eadem mutata resurgo" (Mutante y permanente, vuelvo a resurgir siendo el mismo), aludiendo a las propiedades de la espiral.
En el cementerio de matemáticos de Basilea (Suiza) se puede apreciar su lápida con una espiral, pero desgraciadamente devido a la ignorancia de los canteros que tallaron la "espiral" en su tumba, confundieron la "espiral logaritmica" con la "espiral de Arquimedes".
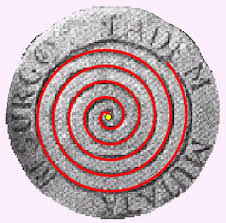

La diferencia entre las dos espirales consiste:
- En la espiral logaritmica, sus arcos aumentan en progresion geométrica, es decir, multiplica en vez de sumar, por lo que cada arco se distancia màs ràpidamente del anterior.
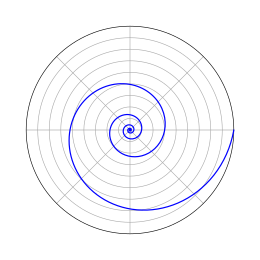
En la naturaleza hay cosas que crecen así, a velocidades constantes, simultáneamente hacia "afuera" y "alrededor" de algo. Es por eso que a la "espiral logarítmica" también se le suele llamar "espiral de crecimiento". Hace millones de años, en la familia de los cefalópodos, había muchas especies de animales con concha en forma de "espiral logaritmica", si observamos la imagen del "Nautilus", cuya concha bisectada, puede apreciarse que está formada por compartimentos separados por tabiques y comunicados por un sifón.



El animal ocupa el compartimento más externo, que es de mayor tamaño, al ir creciendo, el molusco abandona el compartimento anterior y crea uno con la misma forma pero más grande.
- Mientras que en la "espiral de Arquimedes" el aumento de las distancias son constantes, continuas y uniformes.


Arquímedes describió esta espiral en su libro "De las Espirales".

Tambien fue representada en el arte prehistórico irlandés (unos 3000 años a.C).

Alberto Durero, era un pintor del Renacimiento a parte de la pintura su otra pasion eran las matemàticas, en 1525 publicó, una obra titulada: "Instrucción sobre la medida con regla y compàs de figuras planas y sólidas", con este libro intentaba enseñar a los pintores y matemàtios de su época diversos métodos para trazar diferentes figuras geométricas. Durero muestra cómo trazar con regla y compás, es similar a la espiral logarítmica, esta se forma uniendo dos vértices opuestos de los sucesivos cuadrados con un arco de circunferencia, la espiral pasará a la historia con su nombre de la "Espiral de Durero"

Aunque no se trata de una "espiral de Arquímedes" ni de una "espiral logarítmica" pues ninguna de las dos puede construirse con regla y compás, sin embargo se aproxima bastante a esta última.
La espiral logaritmica es la que màs observamos en la naturaleza:
- En las formas de las galaxias como "Andrómeda";

comprender una sola palabra; sin ellos solo se conseguirá vagar por un oscuro
laberinto"
Galileo Galilei
En matemàticas, una espiral es una curva que se inicia en un punto central, y se va alejando progresivamente del centro al mismo tiempo va girando alrededor de él. La "espiral logarítmica" es conocida tambien por el nombre de "espiral de crecimiento", la podemos observar a menudo en la naturaleza.
El primero en hablar de ella fue René Descartes en el año 1638, quien un año después de la publicación de "La Géométrie", se va encontrar con la curva mecánica que responde al problema planteado por Galileo sobre la trayectoria de la caída de un cuerpo atraído por la tierra en rotación.
Descartes en 1638 comunicó sus investigaciones sobre esta curva a Mersenne.

Aunque Descartes y Torricelli habían iniciado su estudio, les faltaba la potente herramienta del cálculo para poder llevar a fin su descubrimiento.
Esto se consiguió en el siglo XVIII, gracias a Jacob Bernouilli, quien le dió el nombre de "espiral logarítmica" se quedó maravillado por la belleza de la figura la bautizó con el nombre de "Spira Mirabilis" (espiral maravillosa), asi tituló su obra dedicada a esta espiral.
Tanto le encantó que dejó escrito en su testamento que, en su lápida debería figurar una espiral logarítmica, y una inscripción en latin que dice:
"Eadem mutata resurgo" (Mutante y permanente, vuelvo a resurgir siendo el mismo), aludiendo a las propiedades de la espiral.
En el cementerio de matemáticos de Basilea (Suiza) se puede apreciar su lápida con una espiral, pero desgraciadamente devido a la ignorancia de los canteros que tallaron la "espiral" en su tumba, confundieron la "espiral logaritmica" con la "espiral de Arquimedes".
La diferencia entre las dos espirales consiste:
- En la espiral logaritmica, sus arcos aumentan en progresion geométrica, es decir, multiplica en vez de sumar, por lo que cada arco se distancia màs ràpidamente del anterior.

En la naturaleza hay cosas que crecen así, a velocidades constantes, simultáneamente hacia "afuera" y "alrededor" de algo. Es por eso que a la "espiral logarítmica" también se le suele llamar "espiral de crecimiento". Hace millones de años, en la familia de los cefalópodos, había muchas especies de animales con concha en forma de "espiral logaritmica", si observamos la imagen del "Nautilus", cuya concha bisectada, puede apreciarse que está formada por compartimentos separados por tabiques y comunicados por un sifón.



El animal ocupa el compartimento más externo, que es de mayor tamaño, al ir creciendo, el molusco abandona el compartimento anterior y crea uno con la misma forma pero más grande.
- Mientras que en la "espiral de Arquimedes" el aumento de las distancias son constantes, continuas y uniformes.


Arquímedes describió esta espiral en su libro "De las Espirales".

Tambien fue representada en el arte prehistórico irlandés (unos 3000 años a.C).

Alberto Durero, era un pintor del Renacimiento a parte de la pintura su otra pasion eran las matemàticas, en 1525 publicó, una obra titulada: "Instrucción sobre la medida con regla y compàs de figuras planas y sólidas", con este libro intentaba enseñar a los pintores y matemàtios de su época diversos métodos para trazar diferentes figuras geométricas. Durero muestra cómo trazar con regla y compás, es similar a la espiral logarítmica, esta se forma uniendo dos vértices opuestos de los sucesivos cuadrados con un arco de circunferencia, la espiral pasará a la historia con su nombre de la "Espiral de Durero"

Aunque no se trata de una "espiral de Arquímedes" ni de una "espiral logarítmica" pues ninguna de las dos puede construirse con regla y compás, sin embargo se aproxima bastante a esta última.
La espiral logaritmica es la que màs observamos en la naturaleza:
- En las formas de las galaxias como "Andrómeda";
- La podemos observar en la forma de la espiral en las borrascas, y en los tornados, sus efectos son devastadores.
- En el reino vegetal: girasoles, margaritas, distribución de las escamas las piñas de piñones o las hojas de una rosa...
- En las conchas de caracolas y moluscos, etc.
- En las telas de araña
Una razón por la que la "espiral logarítmica" aparece en la naturaleza es que es el resultado de esquemas muy simples del crecimiento por ejemplo:
- Crece 1 unidad, dobla 1 unidad
- Crece 2 unidades, dobla 1 unidad
- Crece 3 unidades, dobla 1 unidad...

- Crece 1 unidad, dobla 1 unidad
- Crece 2 unidades, dobla 1 unidad
- Crece 3 unidades, dobla 1 unidad...
La espiral logaritmica, ha sido amenudo utilizada en la arquitectura, para la construcción de campanarios, jardines, avenidas en los jardines de los castillos... en los cuales su forma abierta confiere al edificio una dimensión infinita.






De ahí que meterse en una espiral de vida vertiginosa, es dificil salir.
ResponderEliminarInteresante. Instructivo.
Mis saludos.
Genial!!. Las matemáticas siempre presentes....Qué nos haríamos sin ellas.
ResponderEliminarSaludos
Una belleza de fotografías. Un post muy didáctico como suele ser habitual en ti.
ResponderEliminarEn mi blog tienes algo para ti. De corazón a corazón y me encantaría que lo aceptases
Si no sueles hacerlo no importa es tan solo un ofrecimiento.
Buen finde
http://katy-agradeciendoregalos.blogspot.com/2011/09/premio-de-estoy-tu-lado.html
Preciosas fotografías.
ResponderEliminarmuchas gracias por tu visita
Te dejo mi ternura
Sor.cecilia
Magnífica entrada sobre espirales, muy bien documentada e ilustrada. Aprovecho para saludarte, tras el descanso veraniego; seguiremos en contacto. Abrazos.
ResponderEliminarEstimad- Mariac. Magní fico trabajo.Estoy preparando una expo de fotos de zarcillos de enredaderas y me gustaría imprimir esta información y pegarla en la exposición. Me autorizas?
ResponderEliminarGracias
Luis Levin
Hola Estoy preparando una exposición de fotos de zarcillos y me gustaría imprimir tu blog en la expo. Me autorizas?
ResponderEliminarMuy buena información, ¡gracias!
ResponderEliminarSiempre enamorandome de las matemáticas y su gran lugar en el universo. ¡Qué belleza!
ResponderEliminar